I етап Всеукраїнської олімпіади з математики як засіб розвитку здібностей особистості

Олімпіада — це конкурс, у якому переможцями стають найсильніші, а інші учасники збагачуються новими знаннями і здобувають необхідний досвід.
Традиційно у жовтні кожного року проводяться учнівські олімпіади з навчальних предметів. 12 жовтня відбувся І (шкільний) етап олімпіади з математики у якому взяло участь 39 учнів 6-11 класів. Завдання для проведення олімпіади з математики уклали вчителі предметно-методичної комісії. Після перевірки робіт була сформована команда для участі у ІІ етапі Всеукраїнських олімпіад з математики.
Олімпіади допомагають школярам повірити в себе, наблизитися до більш якісної освіти та зміцнити свій соціальний статус. Цьому передує копітка наполеглива щоденна праця кожного учня.
Завдання для олімпіади з математики 2016
6 клас
- У класі 27 учнів. Чи може кожен з них товаришувати з 9 однокласниками?
- Батькові 29 років, а сину 7 років. Через скільки років батько буде старший за сина в 2 рази?
- Скількома нулями закінчується добуток всіх натуральних чисел від 1 до 100?
- Миколка і Петрик біжать навколо стадіону. Миколці потрібно 3 хвилини, щоб подолати 1 круг, а Петрику – 4 хвилини. Стартували вони одночасно. Через скільки хвилин вони вперше перетнуть лінію старту одночасно?
7 клас
- Після того як пішохід пройшов 1 км і половину шляху, що залишилася, йому ще залишилось пройти третину всього шляху і 1 км. Чому дорівнює весь шлях?
- Довести, що число 49¹⁰⁰-14 ⁵⁰ кратне 5.
- Число 13*045* (де * це цифри)ділиться на72. Знайти це число.
- З дев’яти однакових за зовнішнім виглядом монет одна фальшива (легша). Як за два зважування на шалькових терезах без важків знайти фальшиву монету? Опишіть схему зважування.
9-11 клас
- Член журі та учасник олімпіади грають у таку гру: кожен з них бере по черзі сірники з купки, в якій 2017 сірників. За своїм ходом гравець має взяти 1 або 2 сірники (але не більше, ніж за попереднім своїм ходом). Виграє той, хто бере сірник останнім. Почесне право першого ходу надається учаснику олімпіади. Хто виграє, якщо обидва гравці гратимуть найкращим чином? (Відповідь обґрунтуйте і узагальніть).
- Доведіть, що для кожного натурального числа n(n двійок, та n шісток) виконується нерівність
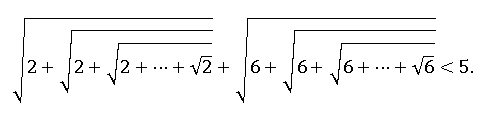
- Точки M, N, K позначено відповідно на сторонах AB, BC, CA гострокутного трикутника ABC так, що ∠ AMK=∠BMN=∠ ACB. Точку перетину відрізків AN і BK позначимо через L. Доведіть, що точки C, K, L, N лежать на одному колі.
- У новосформованому десятому класі деякі учні виявилися вже знайомими між собою, деякі ще ні. В перший день навчання кожна дівчина замріяно подивилася на кожного із знайомих хлопців, тоді як кожен хлопець замріяно подивився на кожну з незнайомих дівчат. Усього було кинуто 117 замріяних поглядів. Скільки у класі хлопців і дівчат, якщо всього не більше за 40 учнів?






Написати коментар:
FaceBook VK Сайт